Какво е формула за множествена регресия?
Формулата за множествена регресия се използва при анализа на връзката между зависими и множество независими променливи и формулата се представя чрез уравнението Y е равно на плюс bX1 плюс cX2 плюс dX3 плюс E, където Y е зависима променлива, X1, X2, X3 са независими променливи , a е отсечка, b, c, d са наклони, а E е остатъчна стойност.
y = mx1 + mx2 + mx3 + b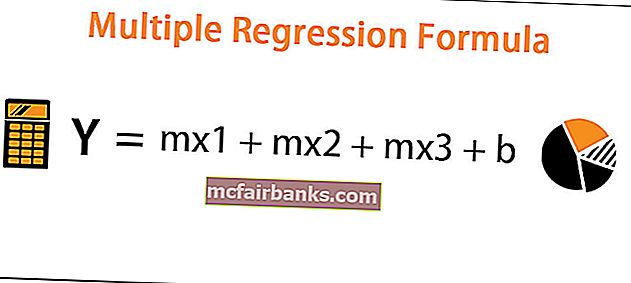
Където,
- Y = зависимата променлива на регресията
- M = наклон на регресията
- X1 = първата независима променлива на регресията
- X2 = втората независима променлива на регресията
- X3 = третата независима променлива на регресията
- B = константа
Обяснение на формулата за анализ на регресия
Множествените регресии са метод за прогнозиране на зависимата променлива с помощта на две или повече независими променливи. Докато провежда този анализ, основната цел на изследователя е да установи връзката между зависимата променлива и независимите променливи. За да се предскаже зависимата променлива, се избират множество независими променливи, които могат да помогнат при предвиждането на зависимата променлива. Използва се, когато линейната регресия не е в състояние да изпълни целта. Регресионният анализ помага в процеса на валидиране дали предикторските променливи са достатъчно добри, за да помогнат при предвиждането на зависимата променлива.
Примери
Можете да изтеглите този шаблон за формула за множествена регресия на Excel тук - Шаблон за формула за множествена регресия в ExcelПример # 1
Нека се опитаме да разберем концепцията за множествен регресионен анализ с помощта на пример. Нека се опитаме да разберем каква е връзката между разстоянието, изминато от шофьор на UBER, и възрастта на шофьора и броя години опит на шофьора.
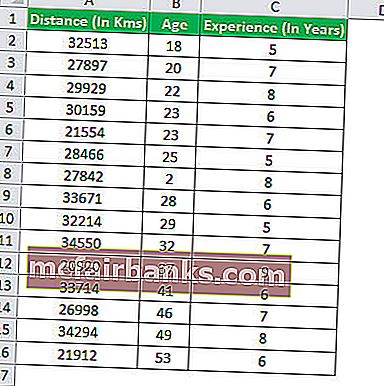
За изчисляване на множествена регресия отидете в раздела Данни в Excel и след това изберете опцията за анализ на данни. За по-нататъшната процедура и изчисляване се отнася до дадената статия тук - Analysis ToolPak в Excel
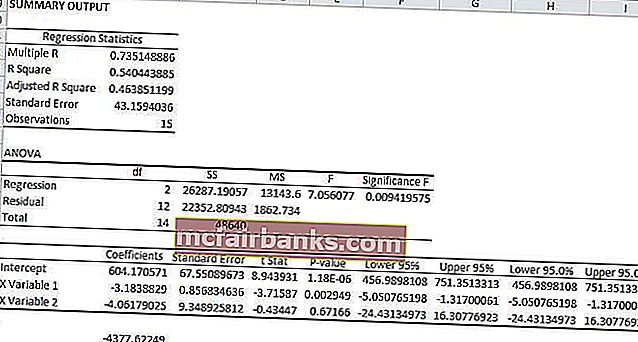
Формулата за регресия за горния пример ще бъде
- y = MX + MX + b
- у = 604,17 * -3,18 + 604,17 * -4,06 + 0
- у = -4377
В този конкретен пример ще видим коя променлива е зависимата променлива и коя променлива е независимата променлива. Зависимата променлива в това уравнение за регресия е разстоянието, изминато от шофьора на UBER, а независимите променливи са възрастта на водача и броят опит, който той има при шофиране.
Пример # 2
Нека се опитаме да разберем концепцията за множествен регресионен анализ с помощта на друг пример. Нека се опитаме да разберем каква е връзката между средния успех на клас ученици и броя часове на обучение и височината на учениците.
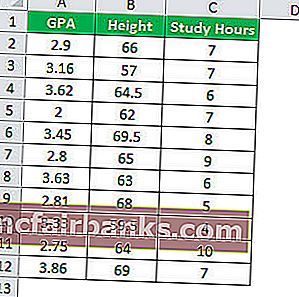
За изчислението отидете в раздела Данни в Excel и след това изберете опцията за анализ на данни.
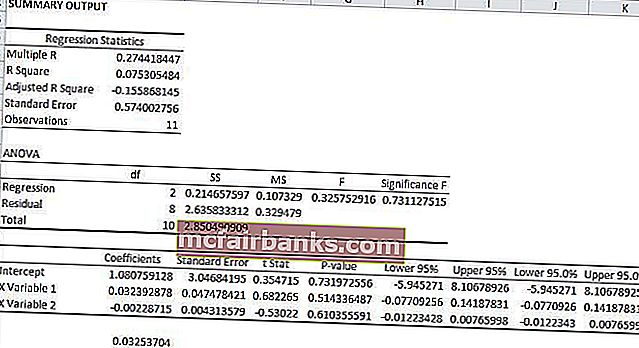
Уравнението на регресията за горния пример ще бъде
y = MX + MX + b
y = 1,08 * .03 + 1,08 * -. 002 + 0
y = .0325
В този конкретен пример ще видим коя променлива е зависимата променлива и коя променлива е независимата променлива. Зависимата променлива в тази регресия е GPA, а независимите променливи са часовете за обучение и височината на студентите.
Пример # 3
Нека се опитаме да разберем концепцията за множествен регресионен анализ с помощта на друг пример. Нека се опитаме да разберем каква е връзката между заплатата на група служители в дадена организация и броя години опит и възрастта на служителите.
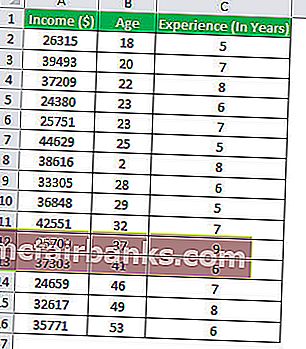
За изчислението отидете в раздела Данни в Excel и след това изберете опцията за анализ на данни.
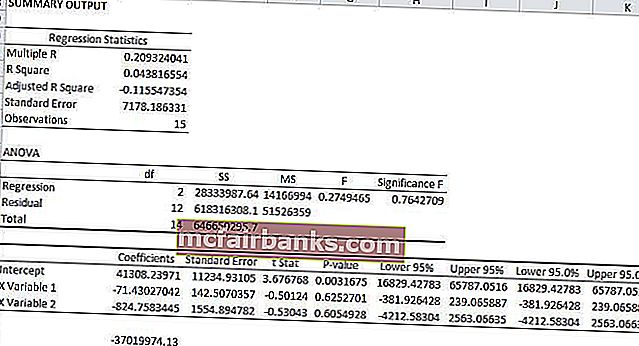
Уравнението на регресията за горния пример ще бъде
- y = MX + MX + b
- y = 41308 * .- 71 + 41308 * -824 + 0
- y = -37019
В този конкретен пример ще видим коя променлива е зависимата променлива и коя променлива е независимата променлива. Зависимата променлива в това уравнение за регресия е заплатата, а независимите променливи са опитът и възрастта на служителите.
Уместност и употреба
Множествените регресии са много полезен статистически метод. Регресията играе много важна роля в света на финансите. Много прогнози се правят с помощта на регресионен анализ. Например продажбите на определен сегмент могат да бъдат прогнозирани предварително с помощта на макроикономически показатели, което има много добра корелация с този сегмент.